(1) Boston vs Carolina (6)
To the surprise of few, the Bruins had little trouble with Montreal in the first round. I'm not sure if this validates the Bruins as a elite team, though. The evidence suggests that the Habs were an average-ish squad that was devastated with injuries, and were therefore not a quality opponent.
The Canes were impressive against the Devils. Not only did they emerge from the series victorious, but they managed to upset one of top teams in the conference without getting noticeably outplayed. While I didn't catch as much of the Canes-Devils series as I would have liked to, the numbers indicate that the shots and scoring chances were fairly even. This bodes well for Carolina, I think, given that the Devils were one of the strongest teams -- if not the strongest team-- in the conference in terms of outshooting and territorial play. Therefore, on account of their first round performance, I think it's fair to say that the Canes are a legitimately good team.
What will likely play to Boston's advantage in this series is the fatigue element -- whereas the Canes have played seven games so far, the Bruins have only played four. They also had a much better goal differential than Carolina over the course of the regular season, and dominated the season series against the Canes (at least outcome wise).
However, I find it hard not to go with Carolina here. Territorially speaking, Carolina was much more dominant than Boston during the regular season, as evidenced by their clear advantage in Corsi. Some might point out that the Bruins surely played more with the lead than the Canes, therefore artificially rendering their EV numbers less impressive. While this is a valid point, Carolina's advantage in Corsi remains true even if one only looks at even strength play when the score is tied. I'm also impressed by Carolina's ability to consistently draw more powerplays than the opposition (Boston was merely average in this regard during the regular season).
While I'm not overly confident about this pick, I've yet to go with an underdog and it would be awfully lame if I were to go with the safe pick in every series. And frankly, the further that the Bruins go, the worse it reflects upon yours truly -- therefore, there's an element of self-interest here too.
Canes in 6
(2) Washington vs Pittsburgh (4)
The Pens had more difficulty with the Flyers than I anticipated. While I personally thought that the balance of play and scoring chances were fairly even, one could make an argument that the Flyers were the better team in that series.
The Capitals-Rangers series was an interesting one. One of the TSN announcers -- Gord Miller, I think -- remarked that, in each of the games, the winning team tended to be the team that got outplayed. I think that this is only partly true. While the winning team was outshot in four of the seven games, I think that at least some of that was due to the trailing team playing desperate hockey and throwing everything on net. In any event, I think that the Capitals demonstrated that they were the better of the two clubs over the course of the series and were thus worthy of advancement.
From my perspective, this series is essentially a coin toss. At first glance, Washington's superior goal differential, better underlying numbers, and home ice advantage makes them the more attractive pick. However, Pittsburgh's underlying numbers and goal differential since the coaching change/return of Gonchar/roster acquisitions are, if pro-rated, on par with that of Washington (or perhaps better). Over the course of a seven game series, home ice advantage is almost negligible (1-3%), but, seeing as how I can't otherwise choose between these two teams, it tilts me in favor of Washington.
Capitals in 7.
(2) Detroit vs Anaheim (8)
Detroit didn't have much difficulty in disposing of the Jackets, although the underlying numbers suggest that the play was more even than the results would imply.
Beating the Sharks in a seven game series is no small feat and Anaheim deserves credit in that respect. However, getting decidedly outshot and outchanced, while giving up a ton of powerplays to the opposition, is never a recipe for long term success. Therefore, without any hesitation, my pick is Detroit.
Wings in Five.
(3) Vancouver vs Chicago (4)
An interesting matchup. Both teams were good at EV throughout the course of the regular season. However, while the Hawks did it through accruing a massive shot differential and dominant territorial play, the Canucks were more reliant on the percentages. Although their impressive EV save percentage is likely sustainable (see: Luongo, Roberto), I'm skeptical as to whether the same is true of their equally impressive shooting percentage. Additionally, while both teams had a positive overall goal differential, Chicago's was better. Therefore, I'll take the Blackhawks.
Hawks in 6.
Wednesday, April 29, 2009
Sunday, April 26, 2009
The Percentages Revisited: 5-on-4 Shooting Percentage
A while back, I wrote about the effect of randomness on even strength* shooting percentage. For those who didn't have an opportunity to read that post, I'll briefly summarize the findings:
1. It would appear that a large portion of the inter-team variation in EV shooting percentage can be accounted for by random variation.
2. The spread among NHL teams is very slightly broader than what would be expected by chance alone. Therefore, it would appear that teams do in fact exert some influence on their EV shooting percentage.
* I actually only looked at 5-on-5 shooting percentage. I assume that the results are generalizable to even strength play as a whole, although that may not be the case.
In making my playoff predictions this year, I looked very closely at each team's shot rate (both SF and SA) in each of the main game situations (that is, 5-on-5, 5-on-4, 4-on-5). I also looked at how often each team had played in each game situation over the course the season. My method of determining the 'better' team basically revolved entirely around these two factors.
My method of evaluation didn't really accord much weight to the percentages, regardless of game state. I did this under the -- somewhat faulty -- assumption that most of the inter-team variation in the percentages is due to randomness. If true, there wouldn't be much point in taking the percentages into account when attempting to predict future results.
As it happens, that really isn't true at all. It appears to largely be true in terms of EV shooting percentage. However, this finding isn't necessarily generalizable to other game states. For one, it doesn't seem to be case for EV save percentage. More on that later.
It also doesn't seem to apply to 5-on-4 shooting percentage. While I began my analysis under the expectation that the majority of the inter-team variation in 5-on-4 shooting percentage could be explained through randomness, that doesn't appear to be true.
My methodology was basically identical to that used in my analysis of 5-on-5 shooting percentage, with one obvious difference -- instead of looking at 5-on-5 play, my focus this time was on 5-on-4 play. Here's a quick explanation of my method.
Firstly, I looked at how many shots each team took at 5-on-4 during the 2008-09 regular season. The values can be viewed at behindthenet. I then figured out the average 5-on-4 shooting percentage in the league (~0.128). I then simulated 100 'seasons'. In each 'season', the number of shots taken by each team was the number of 5-on-4 shots taken by that team during the 2008-09 season. However, the percentage of scoring a goal on each shot for every team was 0.128 -- the league average 5-on-4 shooting percentage. That is, each team was assigned the exact same shooting percentage. This is significant as, in any particular 'season', any deviation from the mean is strictly due to randomness, thus allowing one to determine how the spread in 5-on-4 should appear through the impact of randomness alone.
The results:
 The first graph is fairly straightforward. The blue distribution is the 'predicted' distribution. It represents the spread in 5-on-4 shooting percentage over the course of the 100 simulated seasons. Thus, it's an approximation of what the spread among teams in 5-on-4 shooting percentage would look like if each team had the exact same underlying 5-on4 shooting percentage.
The first graph is fairly straightforward. The blue distribution is the 'predicted' distribution. It represents the spread in 5-on-4 shooting percentage over the course of the 100 simulated seasons. Thus, it's an approximation of what the spread among teams in 5-on-4 shooting percentage would look like if each team had the exact same underlying 5-on4 shooting percentage.
The red distribution is the 'actual' distribution. It represents the spread in 5-on-4 shooting percentage among NHL teams for the 2008-09 regular season. That mini-peak on the far right of the graph represents Philadelphia, who led the league with a gaudy 5-on-4 shooting percentage of 0.181.
 This graph is a 'smoothed' version of the above graph. The blue distribution required no smoothing and is therefore identical to the one above.
This graph is a 'smoothed' version of the above graph. The blue distribution required no smoothing and is therefore identical to the one above.
However, the red distribution did require smoothing. Thus, the red distribution in this graph is simply a normal distribution with a mean of ~0.128 and standard deviation of 0.02. Why 0.02? That was the standard deviation in 5-on-4 shooting percentage among NHL teams during the 2008-09 season.
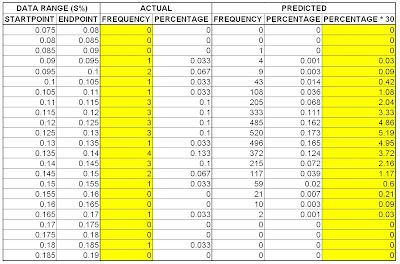 Here's the raw data. It's more or less self-explanatory.
Here's the raw data. It's more or less self-explanatory.
The first two columns are the start and end points for the percentage 'ranges' (it's hard to make sense of non-discrete data). The 'actual' column -- the third one from the left -- shows the numerical distribution in 5-on-4 shooting percentage for the 2008-09 season. So, for example, one team in the NHL had a shooting percentage between 0.18 and 0.185 this season. The 4th column merely shows the relative frequency of the third column values.
In terms of the predicted values, the 5th column shows the frequency of each percentage range for the 100 simulated seasons, while the 6th column expresses those values as a relative frequency. So, for example, out of the 3000 simulated team-seasons (100 seasons * 30 teams = 3000 team-seasons), two teams had a shooting percentage falling between 0.165 and 0.170.
The final column merely shows the numerical distribution in shooting percentage in a hypothetical 30 team league where each team has the same underlying shooting percentage. This allows for a comparison to be made with the actual distribution, shown in the 3rd column.
 Finally, the supplemental data. For each of the 100 simulated seasons, I calculated the standard deviation in shooting percentage among the teams. 'PREDICTED ST DEV MEAN' is the average standard deviation over the 100 seasons. 'PREDICTED ST DEV MIN' is the minimum standard deviation for the 100 seasons. 'PREDICTED ST DEV MAX' is the maximum standard deviation for the 100 seasons. 'ACTUAL ST DEV' is the standard deviation in 5-on-4 shooting percentage among NHL teams for the 2008-09 regular season.
Finally, the supplemental data. For each of the 100 simulated seasons, I calculated the standard deviation in shooting percentage among the teams. 'PREDICTED ST DEV MEAN' is the average standard deviation over the 100 seasons. 'PREDICTED ST DEV MIN' is the minimum standard deviation for the 100 seasons. 'PREDICTED ST DEV MAX' is the maximum standard deviation for the 100 seasons. 'ACTUAL ST DEV' is the standard deviation in 5-on-4 shooting percentage among NHL teams for the 2008-09 regular season.
The fact that the actual standard deviation is larger than the maximum standard deviation for any of the simulated seasons is fairly conclusive proof that randomness alone cannot account for the inter-team variation in 5-on-4 shooting percentage. For what it's worth, when I did my analysis on the effect of randomness on EV shooting percentage, some of the simulated seasons had a larger standard deviation than the actual standard deviation.
Lastly, the final row shows the inter-year correlation -- that is, for 0708 and 0809 -- in 5-on-4 shooting percentage at the team level. The value is non-trivially positive, which lends support to my above finding that teams can reliably influence their 5-on-4 shooting percentage.* Not surprisingly, the Flyers were tied for the league lead in 5-on-4 shooting percentage last season.
*On the other hand, Tyler at mc79hockey, in a post examining this type of thing at the start of the 2008-09 season, found an inter- year correlation that was somewhat lower, on the order of ~0.30.
EDIT:
Also relevant and of interest:
Vic Ferrari, in the comments section of this post -- in which he examines the ability of individuals player to effect PK SV% --, reports that individual Oilers had a substantial effect on powerplay shooting percentage while on the ice. This tends to support the idea that powerplay shooting percentage is highly non-random in its distribution.
1. It would appear that a large portion of the inter-team variation in EV shooting percentage can be accounted for by random variation.
2. The spread among NHL teams is very slightly broader than what would be expected by chance alone. Therefore, it would appear that teams do in fact exert some influence on their EV shooting percentage.
* I actually only looked at 5-on-5 shooting percentage. I assume that the results are generalizable to even strength play as a whole, although that may not be the case.
In making my playoff predictions this year, I looked very closely at each team's shot rate (both SF and SA) in each of the main game situations (that is, 5-on-5, 5-on-4, 4-on-5). I also looked at how often each team had played in each game situation over the course the season. My method of determining the 'better' team basically revolved entirely around these two factors.
My method of evaluation didn't really accord much weight to the percentages, regardless of game state. I did this under the -- somewhat faulty -- assumption that most of the inter-team variation in the percentages is due to randomness. If true, there wouldn't be much point in taking the percentages into account when attempting to predict future results.
As it happens, that really isn't true at all. It appears to largely be true in terms of EV shooting percentage. However, this finding isn't necessarily generalizable to other game states. For one, it doesn't seem to be case for EV save percentage. More on that later.
It also doesn't seem to apply to 5-on-4 shooting percentage. While I began my analysis under the expectation that the majority of the inter-team variation in 5-on-4 shooting percentage could be explained through randomness, that doesn't appear to be true.
My methodology was basically identical to that used in my analysis of 5-on-5 shooting percentage, with one obvious difference -- instead of looking at 5-on-5 play, my focus this time was on 5-on-4 play. Here's a quick explanation of my method.
Firstly, I looked at how many shots each team took at 5-on-4 during the 2008-09 regular season. The values can be viewed at behindthenet. I then figured out the average 5-on-4 shooting percentage in the league (~0.128). I then simulated 100 'seasons'. In each 'season', the number of shots taken by each team was the number of 5-on-4 shots taken by that team during the 2008-09 season. However, the percentage of scoring a goal on each shot for every team was 0.128 -- the league average 5-on-4 shooting percentage. That is, each team was assigned the exact same shooting percentage. This is significant as, in any particular 'season', any deviation from the mean is strictly due to randomness, thus allowing one to determine how the spread in 5-on-4 should appear through the impact of randomness alone.
The results:
 The first graph is fairly straightforward. The blue distribution is the 'predicted' distribution. It represents the spread in 5-on-4 shooting percentage over the course of the 100 simulated seasons. Thus, it's an approximation of what the spread among teams in 5-on-4 shooting percentage would look like if each team had the exact same underlying 5-on4 shooting percentage.
The first graph is fairly straightforward. The blue distribution is the 'predicted' distribution. It represents the spread in 5-on-4 shooting percentage over the course of the 100 simulated seasons. Thus, it's an approximation of what the spread among teams in 5-on-4 shooting percentage would look like if each team had the exact same underlying 5-on4 shooting percentage.The red distribution is the 'actual' distribution. It represents the spread in 5-on-4 shooting percentage among NHL teams for the 2008-09 regular season. That mini-peak on the far right of the graph represents Philadelphia, who led the league with a gaudy 5-on-4 shooting percentage of 0.181.
 This graph is a 'smoothed' version of the above graph. The blue distribution required no smoothing and is therefore identical to the one above.
This graph is a 'smoothed' version of the above graph. The blue distribution required no smoothing and is therefore identical to the one above.However, the red distribution did require smoothing. Thus, the red distribution in this graph is simply a normal distribution with a mean of ~0.128 and standard deviation of 0.02. Why 0.02? That was the standard deviation in 5-on-4 shooting percentage among NHL teams during the 2008-09 season.
 Here's the raw data. It's more or less self-explanatory.
Here's the raw data. It's more or less self-explanatory.The first two columns are the start and end points for the percentage 'ranges' (it's hard to make sense of non-discrete data). The 'actual' column -- the third one from the left -- shows the numerical distribution in 5-on-4 shooting percentage for the 2008-09 season. So, for example, one team in the NHL had a shooting percentage between 0.18 and 0.185 this season. The 4th column merely shows the relative frequency of the third column values.
In terms of the predicted values, the 5th column shows the frequency of each percentage range for the 100 simulated seasons, while the 6th column expresses those values as a relative frequency. So, for example, out of the 3000 simulated team-seasons (100 seasons * 30 teams = 3000 team-seasons), two teams had a shooting percentage falling between 0.165 and 0.170.
The final column merely shows the numerical distribution in shooting percentage in a hypothetical 30 team league where each team has the same underlying shooting percentage. This allows for a comparison to be made with the actual distribution, shown in the 3rd column.
 Finally, the supplemental data. For each of the 100 simulated seasons, I calculated the standard deviation in shooting percentage among the teams. 'PREDICTED ST DEV MEAN' is the average standard deviation over the 100 seasons. 'PREDICTED ST DEV MIN' is the minimum standard deviation for the 100 seasons. 'PREDICTED ST DEV MAX' is the maximum standard deviation for the 100 seasons. 'ACTUAL ST DEV' is the standard deviation in 5-on-4 shooting percentage among NHL teams for the 2008-09 regular season.
Finally, the supplemental data. For each of the 100 simulated seasons, I calculated the standard deviation in shooting percentage among the teams. 'PREDICTED ST DEV MEAN' is the average standard deviation over the 100 seasons. 'PREDICTED ST DEV MIN' is the minimum standard deviation for the 100 seasons. 'PREDICTED ST DEV MAX' is the maximum standard deviation for the 100 seasons. 'ACTUAL ST DEV' is the standard deviation in 5-on-4 shooting percentage among NHL teams for the 2008-09 regular season.The fact that the actual standard deviation is larger than the maximum standard deviation for any of the simulated seasons is fairly conclusive proof that randomness alone cannot account for the inter-team variation in 5-on-4 shooting percentage. For what it's worth, when I did my analysis on the effect of randomness on EV shooting percentage, some of the simulated seasons had a larger standard deviation than the actual standard deviation.
Lastly, the final row shows the inter-year correlation -- that is, for 0708 and 0809 -- in 5-on-4 shooting percentage at the team level. The value is non-trivially positive, which lends support to my above finding that teams can reliably influence their 5-on-4 shooting percentage.* Not surprisingly, the Flyers were tied for the league lead in 5-on-4 shooting percentage last season.
*On the other hand, Tyler at mc79hockey, in a post examining this type of thing at the start of the 2008-09 season, found an inter- year correlation that was somewhat lower, on the order of ~0.30.
EDIT:
Also relevant and of interest:
Vic Ferrari, in the comments section of this post -- in which he examines the ability of individuals player to effect PK SV% --, reports that individual Oilers had a substantial effect on powerplay shooting percentage while on the ice. This tends to support the idea that powerplay shooting percentage is highly non-random in its distribution.
Wednesday, April 15, 2009
Playoff Predictions -- Western Conference
(1) San Jose vs Anaheim (8)
This is a tough matchup for the Sharks. Out of all of the teams that the Sharks could have potentially drawn (NSH, CBJ, MIN, STL, EDM), Anaheim is probably the strongest.
The Sharks started the season on a tear, outshooting and outplaying the opposition like it was nobody's business. Since that time, they've cooled down a bit. They're still consistently outplaying the other team, but not to the degree that they were at the beginning of the year. I'm not sure how important this is, but I know that Matt at Battle of Alberta has been an advocate of excluding a team's first 20 games of the year when assessing each team's chances of playoff success. Perhaps there's something to that.
Anaheim has a formidable powerplay and I think that if they're going to win this series, they're going to have do it on that basis, considering that San Jose is clearly the more dominant team at ES. There are two problems with this, however:
1. If this series sees a lot of special teams play, it might actually benefit the Sharks more, as the Sharks are a much more disciplined team than Anaheim and have a much better PP/PK ratio.
2. The Sharks have the better PK and have a pretty good PP in their own right.
This series won't be an easy win for San Jose by any means, but at the same time it's hard to pick against them.
Sharks in 6.
(2) Detroit vs Columbus (7)
Having browsed through the picks of other bloggers and media personalities, Columbus seems to be a popular pick as an underdog.
From what I've seen, some of the rationale behind the pick is that Columbus will be able to exploit Detroit's weak goaltending situation.
I don't necessarily agree with this reasoning.
Firstly, Detroit has had poor goaltending all season, yet they've still managed to post a much better goal differential than Columbus. That's important.
Secondly, I have a hard time believing that Chris Osgood is as bad as his save percentage would imply. This is same goaltender that posted a 0.914 SV % in the regular season last year and 0.930 SV % in the playoffs. A lot of that had to do with playing behind the league's best team -- his expected save percentage based on shot quality in the playoffs last year was something like 0.94, according to hockeynumbers. However, this years Wings are as good or almost as good as last years squad. True, Osgood is getting up there in age, but I doubt that any age-related decline would be so marked. Save percentage is at least partly random in its distribution and I would expect Osgood's save percentage to gravitate towards the league average in the foreseeable future (i.e. the playoffs).
Thirdly, even if Osgood actually is terrible, then the Wings have the option of playing Conklin in his stead, who's actually been fairly competent this season.
Detroit in 5.
(3) Vancouver vs St. Louis (6)
There isn't a great deal that can be said about this series, but it's obvious to me that Vancouver is the better team and I expect them to advance without too much difficulty.
Not only is Vancouver the better team on paper, and they're also better by virtue of conventional metrics of team strength, like goal differential. Vancouver's underlying numbers are pretty average, although one of the benefits of having a goaltender like Luongo is that it generally allows you to be an EV outscorer without having the shot differential to match.
St. Louis has played well in the second half of the season, but so have the Canucks. Therefore, picking St. Louis on account of their second half play isn't overly logical.
Canucks in 5.
(4) Chicago vs Calgary (5)
A lot of people are discounting the Flames -- even Flames fans themselves, it seems.
One of my earlier posts addressed the fact that the Blackhawks are an interesting team. They have an excellent shot differential, an excellent goal differential, yet are marginally above average in terms of the expected goals numbers at hockeynumbers. I'm not sure how to account for this but I'm thinking that it might have something to do with the "shoot liberally and prevent shots against at all costs" strategy, as historically employed by Joel Quenneville.
As Kent notes, Chicago is a territorially dominant team at even strength, with an aggregate team corsi of 655. However, Calgary has an even better corsi at 778. Thus, both teams perform well here, with there being no clear advantage to either of them.
The difference between these two teams largely relates to goaltending. Whereas Chicago's has been excellent, Calgary's has been below average, even though for some reason I keep hearing Kiprusoff's name brought up when discussing the Vezina. While this will likely work to Chicago's advantage over the course of the series, I'm not sure how sustainable their team save percentage is, considering that they tend to give up such high quality shots against on average.
While I'm not necessarily convinced that Chicago is the better team, their advantage in goal differential is hard to ignore. That, coupled with the Flames injury problems and the fact that they'll be starting this series on the road, tilts the scales in their favor.
Blackhawks in 7.
Monday, April 13, 2009
Playoff Predictions -- Eastern Conference
(1) Boston vs Montreal (8)
I've written before about how I think that the Bruins are not as good as either their goal differential or record would suggest. Now that the season is over, my opinion hasn't really changed. That Boston has managed to post a goal differential of +80, despite having a negative 43 shot differential, suggests that they've been at least somewhat fortunate, and I don’t think that any reasonable person would deny that. Since my original post back in January, it appears that I've been somewhat vindicated. As per timeonice, the Bruins' EV shooting percentage had been 10.3% up to that point, but has only been 7.6% since then. However, their team EV save percentage has remained excellent and, considering that they also excelled in that regard last year, I think that they're the type of team that's going to reliably post a high EV save percentage over the large sample of games. Whether this is due to good goaltending, coaching/team strategy, or some combination thereof, I can't say. Interestingly, it seems that the Bruins have not been any better than the average team in terms of shot quality against this season, which implicates good goaltending as the causal factor (see here, for example).

For those that value the underlying numbers more than the results, special teams are a wash. But at even strength, the Bruins are much better any way you look at it.
The Habs were actually playing pretty well throughout the first part of the season, but since then they’ve fallen off the proverbial cliff. Both their goal and shot differential have dropped precipitously. I’d be inclined to attribute this to injuries, but they were also missing some guys during the first half and it didn’t seem to have too great of an impact upon their play.
Although I wouldn't necessarily be shocked if
Bruins in 5.
(2) Washington vs New York Rangers (7)
The Rangers are another team that I've written about over the course of the season. In hindsight, my appraisal may have been a tad harsh. I seemed to have overlooked the fact that the Rangers had given up a tonne of shorthanded goals at the time, which tends to suggest bad luck. Since then, the Rangers have undergone a coaching range which, like in the case of the Penguins, seems to have helped them to some degree -- though perhaps moreso in terms of their results than their actual play.
Even though the Rangers are respectable, the Capitals seem to be the better team. They're better than the Rangers at EV strength and much better on the powerplay. The Rangers appear to have the penalty kill but the advantage is too small for it to make up for their other deficiencies. Some may point out that the Rangers have the better goaltending, and while this probably true, goaltending is only really important to the extent that it contributes to goal differential. The Capitals have a much better GD than the Rangers. I realize that there's a tendency in the hockey world to treat goaltending as more important in the playoffs, but I've never seen any evidence that would support that notion. I suspect that it's neither more nor less important than during the regular season.Capitals in 6.
(3) New Jersey vs Carolina (6)
A fairly strong argument can be made that the Devils are the class of the East. Their underlying numbers are fantastic, especially at EV and on the powerplay. Additionally, it's difficult on paper to find any source of weakness with the team.
My choice, therefore, is not a difficult one, and while
Devils in 6.
(4) Pittsburgh vs Philadelphia (5)
I've been meaning to make a post about the turnaround that the Pens have experienced since their coaching change. Not only have they substantially improved their record, but -- and more importantly -- their underlying numbers as well. Observe: I realize that this might appear a bit contradictory, given what I wrote above. However, unlike in the case with
Penguins in 5.
Subscribe to:
Posts (Atom)
